いろいろ (a+b)^3 expansion formula 243486-(a+b+c)^3 expansion formula
Play this game to review Algebra I Find the coefficient of x 3 in the expansion of (1 x) Preview this quiz on Quizizz Find the coefficient of x3 in the expansion of (1 x) Binomial Expansion a 5 5a 4 b 10a 3 b 2 10a 2 b 3 5ab 4 b 5 a 5 5a 4 b 10a 3 b 2 10a 2 b 3 5ab 4 b 5 a 5 − 5ab 10ab − 10ab 5abThus the coefficient of superficial expansion is twice the coefficient of linear expansion Relation Between α and γ Consider a thin rectangular parallelopiped solid of length, breadth, height, and volume l 0 , b 0 , h 0 , and V 0 at temperature 0 °CPrecalculus The Binomial Theorem The Binomial Theorem 1 Answer

Expansion Formulae Full Chapter 5 Std 8th I Expansion Formula Class 8th I Maths Chapter 5 Std 8th Youtube
(a+b+c)^3 expansion formula
(a+b+c)^3 expansion formula-In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive integer dependingQ = (x 2;y 2) you can obtain the following information 1The distance between



Expanding Algebraic Expressions Using Identities Worksheets
For the sum of cubes, the "minus" sign goes in the quadratic factor, a 2 – ab b 2Precalculus The Binomial Theorem The Binomial Theorem 1 AnswerWe want to get coefficient of a 3 b 2 c 4 d this implies that r 1 = 3, r 2 = 2, r 3 = 4, r 4 = 1, ∴ The coefficient of a 3 b 2 c 4 d is (10)!/(3!2!4) (1) 2 (1)4 = Question 12 Find the coefficient of in the expansion of (1 x x 2 x 3) 11 Solution By expanding given equation using expansion formula we can get the
What is (ab)^3 Formula?To find an expansion for (a b) 8, we complete two more rows of Pascal's triangle Thus the expansion of is (a b) 8 = a 8 8a 7 b 28a 6 b 2 56a 5 b 3 70a 4 b 4 56a 3 b 5 28a 2 b 6 8ab 7 b 8 We can generalize our results as follows The Binomial Theorem Using Pascal's TriangleSome Example of Binomial Expansion $(a b)^2 = a^2 2ab b^2$ $(a b)^3 = a^3 3a^2b 3ab^2 b^3$ $(a b)^4 = a^4 4a^3b 6a^2b^2 4ab^3 b^4$ $(a b)^5 = a^5 5a^4b 10a^3b^2 10a^2b^3 5ab^4 b^5$ $(a b)^6 = a^6 6a^5b 15a^4b^2 a^3b^3 15a^2b^4 6ab^5 b^6$
How do you use the binomial formula to expand #(x1)^3#?Related Documents Binomial Theorem Binomial theorem for positive integers;Introduction to a minus b whole cube identity with example problems and proofs to learn how to derive ab whole cube formula in mathematics
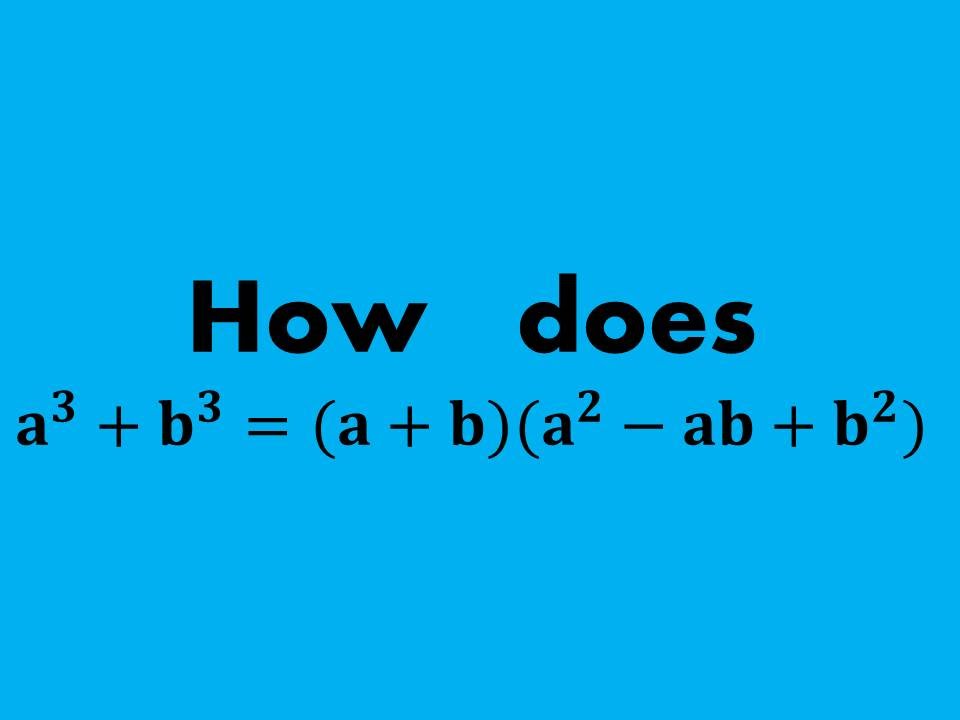


Proof How To Prove The Sum Of Two Cubes A 3 B 3 A B A 2 Ab B 2 Youtube



5 Expansion Of Formulae Practice Set 5 3 8th Maths Maharashtra Board By Sgt Classes Youtube
= (a b)(a b)(a b) = (a b)(a² ab ab b²) = (a b)(a² 2ab b²) = a³ 2a²b ab² a²b 2ab² b³ = a³ 3a²b 3ab² b³The binomial expansion of a difference is as easy, just alternate the signs (x y) 3 = x 3 3x 2 y 3xy 2 y 3In general the expansion of the binomial (x y) n is given by the Binomial TheoremTheorem 671 The Binomial Theorem top Can you see just how this formula alternates the signs for the expansion of a difference?First, I note that they've given me a binomial (a twoterm polynomial) and that the power on the x in the first term is 3 so, even if I weren't working in the "sums and differences of cubes" section of my textbook, I'd be on notice that maybe I should be thinking in terms of those formulas Looking at the other variable, I note that a power of 6 is the cube of a power of 2, so the other



Expansion Formulae Std 8th Practice Set 5 2 I Chapter 5 Expansion Formulae Class 8 I Part 1 Youtube



Solved 3 12 Total Points In This Problem You May Use T Chegg Com
Exercise 3 Expand the following expression, writing your answer in its simplest form Be careful of notation and do not use spaces in your answer ( x ) 2 = x 2 xThe following are algebraix expansion formulae of selected polynomials Square of summation (x y) 2 = x 2 2xy y 2 Square of difference (x y) 2 = x 2 2xy y 2 Difference of squares x 2 y 2 = (x y) (x y) Cube of summation (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Summation of two cubes x 3 y 3 = (x y) (x 2 xy y 2) Cube(a − b) 3 = a 3 b 3 3ab(a b) a 3 − b 3 = (a − b) (a 2 b 2 ab) a 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3(a b)(b c)(c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abc


Q Tbn And9gcsxj6nch9jkvcgw2jprateqxk Fehjaprpo Txh0pvbjcp 2po Usqp Cau



A B 3 Expansion Formula
Formula (a b) 3 = a 3 b 3 3 a b (a b)Introduction to a minus b whole cube identity with example problems and proofs to learn how to derive ab whole cube formula in mathematicsSo the answer is 3 3 3 × (3 2 × x) 3 × (x 2 × 3) x 3 (we are replacing a by 3 and b by x in the expansion of (a b) 3 above) Generally It is, of course, often impractical to write out Pascal"s triangle every time, when all that we need to know are the entries on the nth line


Math Help Algebra Quick Algebra Formulae Technical Tutoring



Binomial Theorem Wikipedia
For example, when n = 5, each term in the expansion of (a b) 5 will look like this a 5 − k b k k will successively take on the values 0 through 5 (a b) 5 = a 5 a 4 b a 3 b 2 a 2 b 3 ab 4 b 5 Note Each lower index is the exponent of b The first term has k = 0 because in the first term, b appears as b 0, which is 1Of course, the power of Taylor's Formula is that we can use it to obtain higherorder poly 3 f (a,b) = 3x fxxx 3x yfxxy 3xy2fxyy y3fyyy It turns out that you can easily get the coecients of the expansion from Pascal's Triangle 1 11 121 1331Related Topics Mathematics Mathematical rules and laws numbers, areas, volumes, exponents, trigonometric functions and more ;
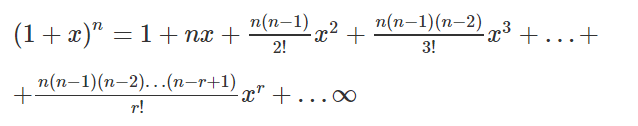


Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf


What Is The Formula Of Math A B 3 Math Quora
Expansion of Integers in an Integer Base This is pretty basic all integers and even real numbers have a decimal expansion, (also, a decimal representation)For example, say, \(568 = 5\times 10^{2}6\times 10^{1} 8\times 10^{0}\)What Is The Expansion Of A B C 3 Quora For more information and source, see on this link https//wwwquoracom/Whatistheexpansionofabc3Discrete Data Sets Mean, Median and Mode Values Calculate arithmetic mean



Question Video Finding A Certain Term In A Binomial Expansion



Expanding Algebraic Expressions Using Identities Worksheets
Precalculus The Binomial Theorem The Binomial Theorem 1 AnswerIn this section, you will learn the formula or expansion for (a 3 b 3)We already know the formula/expansion for (a b) 3 That is, (a b) 3 = a 3 b 3 3ab(a b) Case 1 (a b) 3 = a 3 b 3 3ab(a b) Subtract 3ab(a b) from each sideHow do you use the binomial formula to expand #(x1)^3#?


Factorials To Binomial Theorem
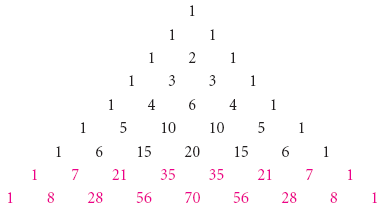


The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
It is a powerful tool for the expansion of the equation which has a vast use in Algebra, probability, etc Binomial Theorem Expansion In binomial theorem expansion, the binomial expression is most important in an algebraic equation which holds two different terms Such as a b, a 3 b 3, etc Let's consider;Http//wwwfreemathvideoscom In this video playlist I will show you the basics for polynomial functions We will start with factoring polynomial equationsThen notice that each formula has only one "minus" sign The distinction between the two formulas is in the location of that one "minus" sign For the difference of cubes, the "minus" sign goes in the linear factor, a – b;



What Is The Correct Formula Of Math A B 3 Math Quora


X A X B X C Expand And Simplify Youtube
What is A3 formula a³ b³ = (a b)(a² – ab b²) you know that (a b)³ = a³ 3ab(a b) b³X, y ∈ R;A^3b^3 Formula (ab)^2 (abc)^2 (a – b)^3 = a^3 – 3a^2b 3ab^2 – b^3 a^3 – b^3 = (a – b)(a^2 ab b^2)


What Is The Expansion Of A B C 3 Quora
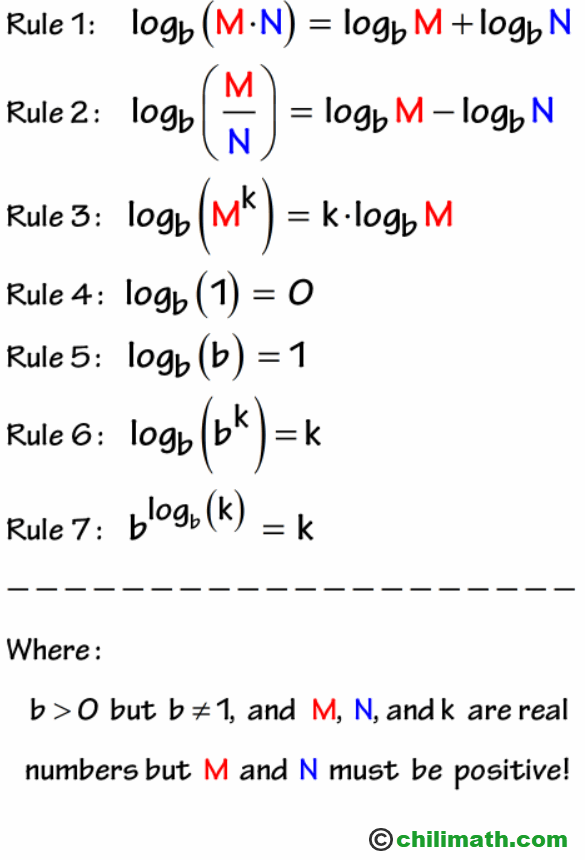


Expanding Logarithms Chilimath
A B C 3 Formula Source(s) https//shrinkurlim/badse 0 0 DanielM Lv 4 1 decade ago This is just multiplying out and bookkeeping It's a^3 b^3 c^3 plus 3 of each term having one variable and another one squared like ab^2, b^2c, all 6 combinations of those, then plus 6abc and that's it 0 53 Quadratic Formula Finally, the quadratic formula if a, b and c are real numbers, then the quadratic polynomial equation ax2 bx c = 0 (31) has (either one or two) solutions x = b p b2 4ac 2a (32) 4 Points and Lines Given two points in the plane, P = (x 1;y 1);You can check the formulas of A plus B plus C Whole cube in three ways We are going to share the (abc)^3 algebra formulas for you as well as how to create (abc)^3 and proof we



Binomial Theorem



Taylor Series Expansion
Introduction to a plus b whole cube formula with example problems with proofs to learn how to derive ab whole cube identity in mathematicsFactorisea^3 b^3 C^3 3abc Get the answer to this question by visiting BYJU'S Q&A ForumFor example, when n = 5, each term in the expansion of (a b) 5 will look like this a 5 − k b k k will successively take on the values 0 through 5 (a b) 5 = a 5 a 4 b a 3 b 2 a 2 b 3 ab 4 b 5 Note Each lower index is the exponent of b The first term has k = 0 because in the first term, b appears as b 0, which is 1



Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5



Answered 3 Using The Taylor Expansion Formula Bartleby
The expansion of (ab)^3 is(ab)^3 (a b)^3 ( a b ) ^ 3 ( a b ) ^ 3 and this will go on for ever Just write the expression on your page and see the miracleA Plus B Plus C Whole cube Are you looking for A plus B plus C Whole cube?There are other ways of solving a quadratic equation instead of using the quadratic formula, such as factoring (direct factoring, grouping, AC method), completing the square, graphing and others Given a general quadratic equation of the form ax²bxc=0 with x representing an unknown, a, b and c representing constants with a ≠ 0, the
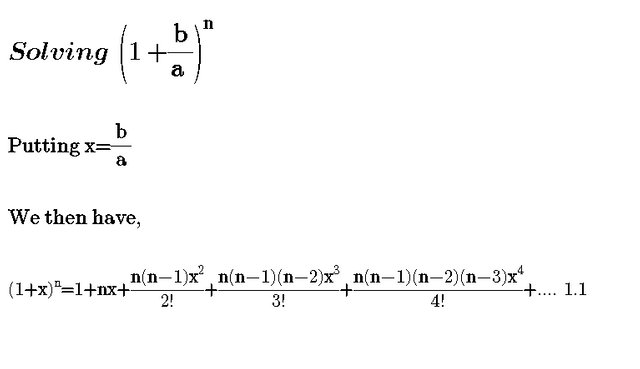


Deriving Of Binomial Expansion Formula For Two Variables A B N Steemit



Expansion Formulae Full Chapter 5 Std 8th I Expansion Formula Class 8th I Maths Chapter 5 Std 8th Youtube
The following are algebraix expansion formulae of selected polynomials Square of summation (x y) 2 = x 2 2xy y 2 Square of difference (x y) 2 = x 2 2xy y 2 Difference of squares x 2 y 2 = (x y) (x y) Cube of summation (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Summation of two cubes x 3 y 3 = (x y) (x 2 xy y 2) CubeComplex Numbers Complex numbers are used in alternating current theory and in mechanical vector analysis;Some Example of Binomial Expansion $(a b)^2 = a^2 2ab b^2$ $(a b)^3 = a^3 3a^2b 3ab^2 b^3$ $(a b)^4 = a^4 4a^3b 6a^2b^2 4ab^3 b^4$ $(a b)^5 = a^5 5a^4b 10a^3b^2 10a^2b^3 5ab^4 b^5$ $(a b)^6 = a^6 6a^5b 15a^4b^2 a^3b^3 15a^2b^4 6ab^5 b^6$


2



What Is The Formula Of Math A B 3 Math Quora
Binomial Theorem – Explanation & Examples A polynomial is an algebraic expression made up of two or more terms which are subtracted, added or multiplied A polynomial can contain coefficients, variables, exponents, constants and operators such addition and subtraction There are three types of polynomials, namely monomial, binomial and trinomial A monomial is an algebraicIn mathematics, a trinomial expansion is the expansion of a power of a sum of three terms into monomialsThe expansion is given by ( ) = ∑ =,, (,,),where n is a nonnegative integer and the sum is taken over all combinations of nonnegative indices i, j, and k such that i j k = n The trinomial coefficients are given by (,,) =!!!!This formula is a special case of the multinomialThe calculator will find the binomial expansion of the given expression, with steps shown Show Instructions In general, you can skip the multiplication sign, so `5x` is equivalent to `5*x` In general, you can skip parentheses, but be very careful e^3x is `e^3x`, and e^(3x) is `e^(3x)`
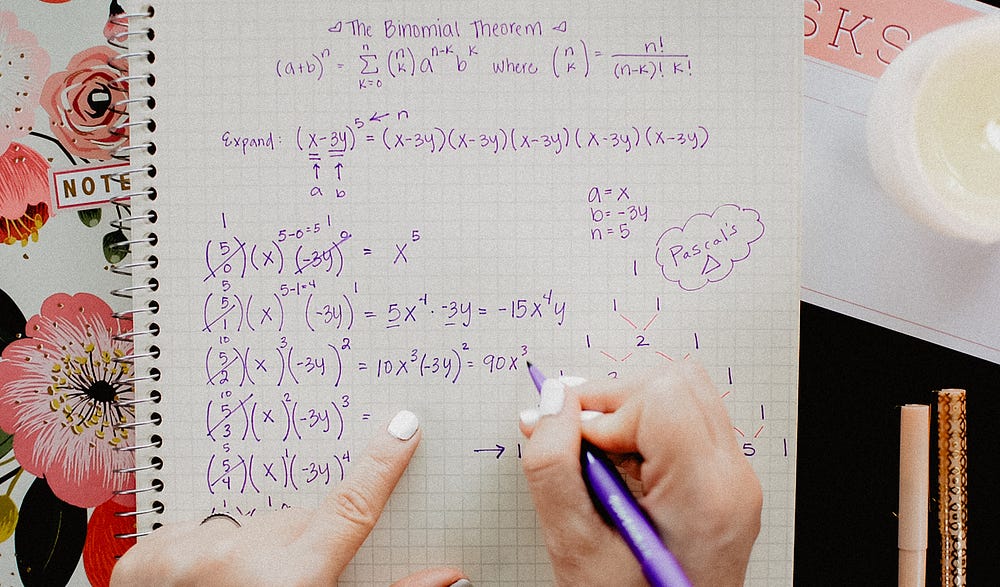


The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
Expand using Pascal's Triangle (ab)^6 Pascal's Triangle can be displayed as such The triangle can be used to calculate the coefficients of the expansion of by taking the exponent and addingDefinition binomial A binomial is an algebraic expression containing 2 terms For example, (x y) is a binomial We sometimes need to expand binomials as follows (a b) 0 = 1(a b) 1 = a b(a b) 2 = a 2 2ab b 2(a b) 3 = a 3 3a 2 b 3ab 2 b 3(a b) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4(a b) 5 = a 5 5a 4 b 10a 3 b 2 10a 2 b 3 5ab 4 b 5Clearly, doing this byIn this section, you will learn the formula or expansion for (a 3 b 3)We already know the formula/expansion for (a b) 3 That is, (a b) 3 = a 3 b 3 3ab(a b) Case 1 (a b) 3 = a 3 b 3 3ab(a b) Subtract 3ab(a b) from each side



Expanding Algebraic Expressions Using Identities Worksheets


What Is The Formula Of Math A 3 B 3 Math Quora
If a b = 12 and a 3 b 3 = 468, then find the value of ab Solution To find the value of ab, we can use the formula or expansion for (a b) 3 Write the formula / expansion for (a b) 3 (a b) 3 = a 3 3a 2 b 3ab 2 b 3 or (a b) 3 = a 3 b 3 3ab(a b) Substitute 12 for (a b) and 468 for (a 3 b 3)How do you use the binomial formula to expand #(x1)^3#?



A B 3 Expansion Formula
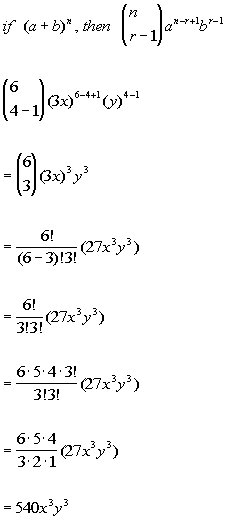


Wtamu Math Tutorials And Help
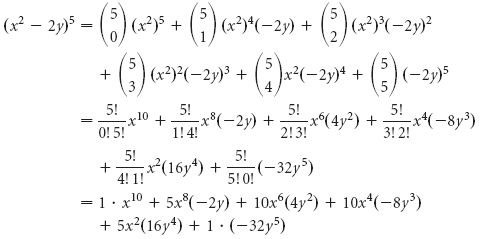


The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets



Binomial Theorem Examples Solutions Examples Videos Worksheets Activities



Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning



Yismxplusc Geometric Proof Of The Cubic Formula A B 3


What Is The Formula Of Math A 3 B 3 Math Quora



Jeff Mccalla Experiments In Learning By Doing



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo



Expansion Formulae Chapter 5 A B 3 A3 3a2b 3ab2 Cbse Ncert State Board Icse Class 8 Youtube



What Is A B 3 Quora



General And Middle Term Binomial Theorem Formula Videos Examples


Standard Identities Of Binomials And Trinomials Equations Examples



Binomial Expansion Using A General Formula Quick Visual Summary With Space For Students To Really Embed T Binomial Theorem This Or That Questions The Expanse


Illustrations Of Formulas
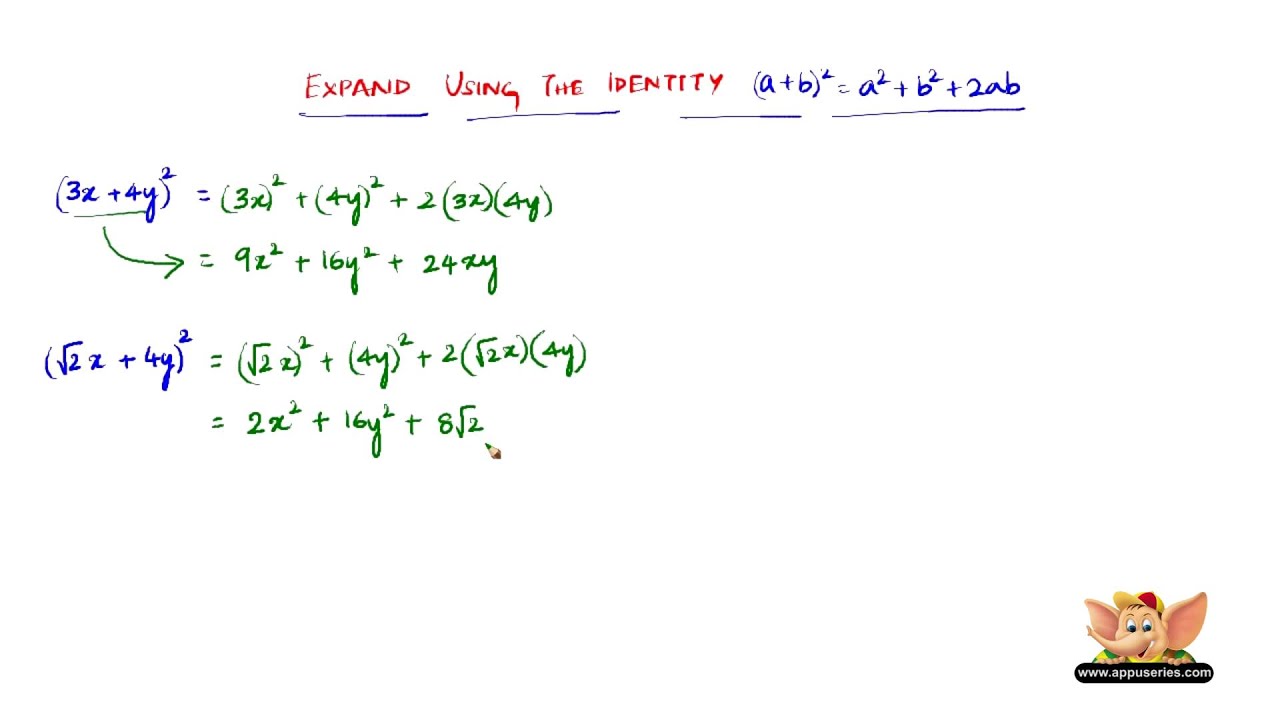


How To Expand Using The Identity A B 2 B2 2ab Youtube



Solved 6 Find The Following Determinants Using The Cofac Chegg Com
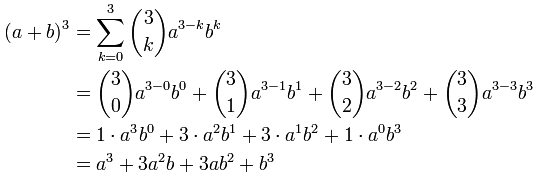


Binomial Theorem



Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf


4 The Binomial Theorem
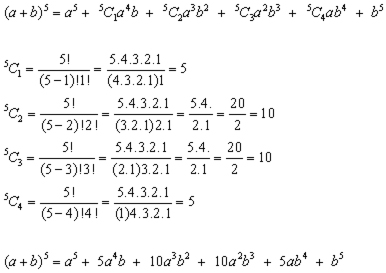


The Binomial Theorem Algebra Pure Mathematics From A Level Maths Tutor
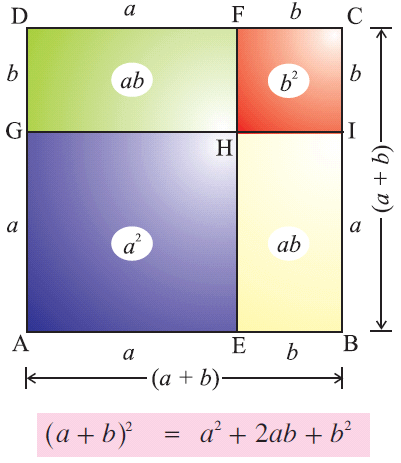


Formula For A Plus B Whole Square



Find The Cube Of 43 Using Expanded Form Of A B 3 Brainly In


What Is The Formula Of Math A B 3 Math Quora



Misc 1 Find A B N In Expansion Of A B N If First Three



Intro To The Binomial Theorem Video Khan Academy


Q Tbn And9gcrsvuubea2fyxbqdbdryxieweephs6lq6mbtcip97hxwvgag Ap Usqp Cau



Algebra Formula Definition Formulas And Examples



3 Expand With The Help Of Formula X Y 3 2



A B N And A B N Formula Expander



Pascal S Triangle And The Binomial Theorem X Y 0 1 X Y 1 1x 1y X Y 2 1x 2 2xy 1y 2 X Y 3 1x 3 3x 2 Y 3xy 2 1 Y 3 X Ppt Download


A B C 3 Formula Expansion


What Is A B 3 Quora


What Is The Formula Of Math A 3 B 3 Math Quora



Simple Proof Of A B A 3a B 3ab B A B 3ab A B And A B A 3a B 3ab B A B 3ab A B Youtube



Msbshse Solutions For Class 8 Maths Part 1 Chapter 5 Expansion Formulae Download For Free



The First Two Terms In A Binomial Expansion Are Shown Below Math A B 3 8 12 E X Ldots Math Find A And B Homework Help And Answers Slader



Solved A Let N 3 Expand Out All The Terms In This Expr Chegg Com



Pascal S Triangle And The Binomial Theorem
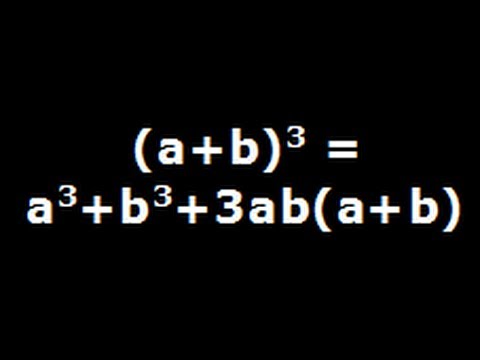


A Plus B Cube Algebra Identity Explained Step By Step Youtube



11 10 The Binomial Formula Recall A B 2 A 2 2ab B 2 For Any Binomial Expansion A B N There Are N 1 Terms Each Term Is N Th Degree Ppt Download



Binomial Theorem Wikipedia



Multinomial Expansion



8th Math Practice Set 5 2 Expansion Formulae Youtube



How To Develop A Numerical Differentiation Formula Using Taylor Expansion Series Mathematics Stack Exchange



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
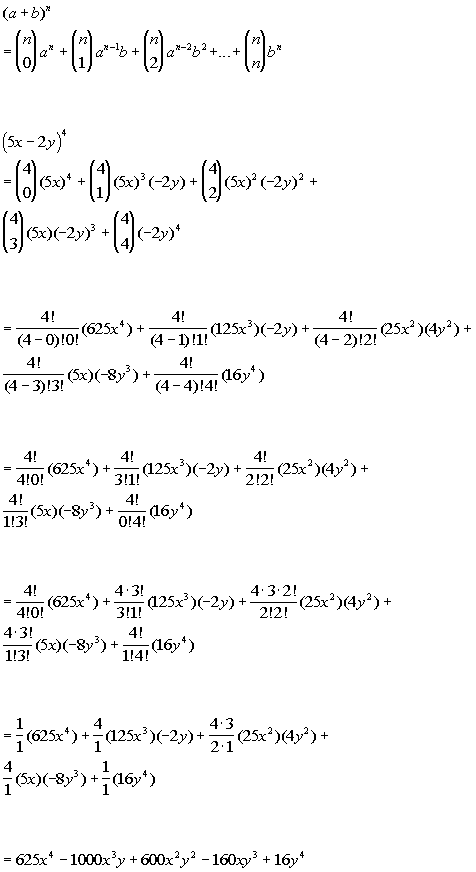


Wtamu Math Tutorials And Help
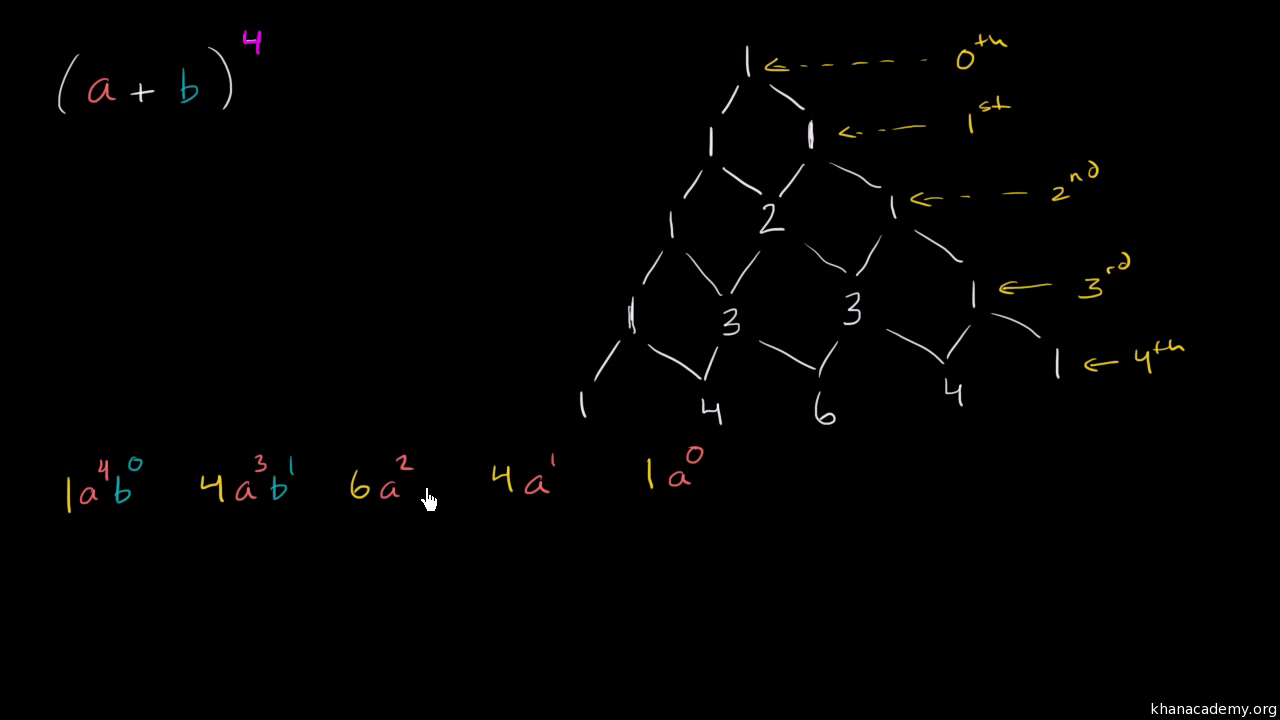


Pascal S Triangle And Binomial Expansion Video Khan Academy



C7eeganit Pages 101 114 Flip Pdf Download Fliphtml5



Selina Concise Mathematics Class 9 Icse Solutions Expansions Including Substitution A Plus Topper



Answer Plese All 4 Matching Pair Match The Following 3 Expand A 2 A Va Ctorize Xi 9x Math Expansion Formulae Meritnation Com



Binomial Theorem
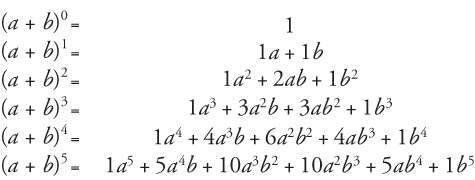


Binomial Coefficients And The Binomial Theorem


Search Q Pascal S Triangle Tbm Isch



Algebra Assessment Solutions Algebra And
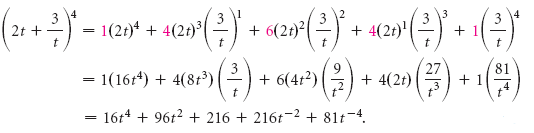


The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets



What Is The Expansion Of A B C 3 Quora



Binomial Expansion Formula Examples Solutions Worksheets Videos Activities


3 Binomial Theorem Ghci Grade 12 Mathematics Of Data Management



Pascal S Triangle



Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf


Q Tbn And9gcrswdldblxmiitn Ggstx6knbcgxw3sex0r673zeswoh Igfkvn Usqp Cau



Expanding Algebraic Expressions Using Identities Worksheets
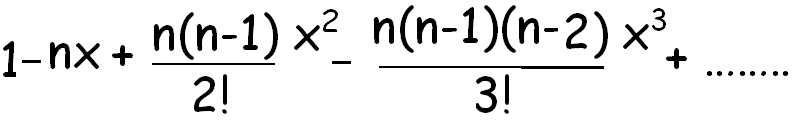


Binomial Expansion Formula For 1 Plus X Whole Power N



A B 3 Expansion Formula



A B Formula Identity


What Is The Formula Of Math A B 3 Math Quora



How To Expand A3 Brainly In


Algebra Expansion Formulae Calculator



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo


Solution Use The Binomial Theorem To Expand The Binomial And Express The Result In Simplified Form X 4 3



Expanding Algebraic Expressions Using Identities Worksheets



Chapter 5 Expansion Of Formulae A B 3 A3 3a2b 3ab2 Class 8 Part 3 Maharashtra Board M Cube Youtube
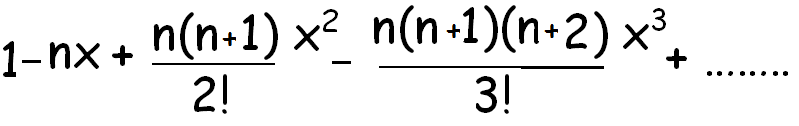


Binomial Expansion Formula For 1 Plus X Whole Power N


コメント
コメントを投稿